ESCHER, GENIO DELLA MATEMATICA O “SEMPLICE” ARTISTA VISIONARIO?

“Per me resta aperta la questione se [questo lavoro]
appartenga al regno della matematica o a quello dell’arte.”

M.C.Escher

Escher nacque a Leeuwarden, Olanda, nel 1898 e quando era a scuola la sua famiglia progettò che seguisse la carriera di architetto del padre. Tuttavia, i brutti voti e un’attitudine per il disegno e la progettazione alla fine lo portarono a una carriera nelle arti grafiche, specializzandosi in xilografie, mezzetinte e litografie. Il suo lavoro passò quasi inosservato fino agli anni ’50, ma nel 1956 tenne la sua prima mostra importante e fu recensito dalla rivista Time, acquisendo una reputazione mondiale. Tra i suoi più grandi ammiratori vi erano i matematici, che riconoscevano nel suo lavoro una straordinaria visualizzazione dei principi matematici. Ciò era ancora più notevole in quanto Escher non aveva ricevuto una formazione matematica formale oltre la scuola secondaria. Mentre il suo lavoro si sviluppava, trasse grande ispirazione dalle idee matematiche di cui leggeva, catturando alla fine l’essenza delle geometrie non euclidee, come vedremo in seguito. Era anche affascinato dai paradossi e dalle figure “impossibili”, e usò un’idea di Roger Penrose (matematico e fisico britannico del ‘900) per sviluppare molte opere d’arte intriganti.

Dal punto di vista prettamente matematico, l’opera di Escher comprende 2 grandi filoni: la geometria dello spazio e quella che potremmo chiamare la logica dello spazio.

Tassellature

Le divisioni regolari del piano, chiamate tassellazioni, sono disposizioni di forme chiuse che coprono completamente il piano senza sovrapporsi e senza lasciare spazi vuoti. In genere, le forme che compongono una tassellazione sono poligoni o forme regolari simili, come le piastrelle quadrate spesso utilizzate sui pavimenti. Escher, tuttavia, era affascinato da ogni tipo di tassellazione, regolare e irregolare, e traeva particolare piacere da quelle che chiamava “metamorfosi”, in cui le forme cambiavano e interagivano tra loro, e talvolta si liberavano persino dal piano stesso. Il suo interesse iniziò nel 1936, quando viaggiò in Spagna e vide i motivi delle piastrelle usati nell’Alhambra (sotto in figura). le creature tassellate giocano ad evadere dalla prigione delle due dimensioni e si aggirano sbuffando sulla scrivania, per poi ricadere di nuovo nel motivo. Escher ha utilizzato questo motivo di rettili in molte tassellazioni esagonali.

I matematici hanno dimostrato che di tutti i poligoni regolari, solo il triangolo, il quadrato e l’esagono possono essere usati per una tassellazione. Escher sfruttò questi schemi di base nelle sue tassellature, applicando ciò che i geometri chiamerebbero riflessioni, riflessioni di scorrimento, traslazioni e rotazioni per ottenere una maggiore varietà di schemi, distorcendo le forme di base per trasformarle in animali, uccelli e altre figure. I risultati possono essere sorprendenti.

Nella figura di sopra per creare gli uccelli viene utilizzata una tassellazione con triangoli…riuscite a vederli?

Nell’opera Rettili le creature tassellate giocano ad evadere dalla prigione delle due dimensioni e si aggirano sbuffando sulla scrivania, per poi ricadere di nuovo nel motivo. Escher ha utilizzato questo motivo di rettili in molte tassellazioni esagonali (sotto in figura).

Poliedri

I solidi regolari, noti come poliedri, esercitavano un certo fascino su Escher. Esistono cinque poliedri con facce poligonali e sono detti solidi platonici: tetraedro (4 facce triangolari), cubo (6 facce quadrate), ottaedro (8 facce triangolari), dodecaedro (12 facce pentagonali) e icosaedro (20 facce triangolari)

Escher si diverte a giocare con questi solidi, stellandoli (ovvero sostituendo ciascuna loro faccia con una piramide, figura in basso a destra ) o intersecandoli. Una delle più interessanti opere in questo senso è l’incisione su legno Stars ( figura in basso a sinistra). Qui ci sono solidi costruiti con ottaedri, tetraedri e cubi intersecanti, tra molti altri. Ci si potrebbe fermare a considerare che se Escher avesse semplicemente disegnato un mucchio di forme matematiche e si fosse fermato lì, probabilmente non avremmo mai sentito parlare di lui o del suo lavoro. Invece, con espedienti come il posizionamento dei camaleonti all’interno del poliedro per prenderci in giro e allarmarci, Escher ci scuote dalle nostre comode abitudini percettive e ci sfida a guardare con occhi nuovi le cose che ha creato.

La forma dello spazio

Tra le opere più importanti di Escher dal punto di vista matematico ci sono quelle che trattano della natura dello spazio stesso. Escher creò molte belle rappresentazioni dello spazio iperbolico, come nella xilografia Circle Limit III.(figura in basso)

Questo è uno dei due tipi di spazio non euclideo e il modello rappresentato nell’opera di Escher è in realtà dovuto al matematico francese Poincaré.

Per farti un’idea di come sia questo spazio, immagina di essere realmente nel quadro stesso. Mentre cammini dal centro del quadro verso il suo bordo, ti rimpicciolirai proprio come fanno i pesci nell’immagine, così che per raggiungere effettivamente il bordo devi camminare per una distanza che, a te, sembra infinita. In effetti, per te, essendo all’interno di questo spazio iperbolico, non dovrebbe essere immediatamente ovvio che ci sia qualcosa di insolito in esso: dopotutto, devi camminare per una distanza infinita per arrivare al bordo anche dello spazio euclideo ordinario. Tuttavia, se fossi un attento osservatore potresti iniziare a notare alcune cose strane, come il fatto che tutti i triangoli simili hanno le stesse dimensioni e che nessuna figura rettilinea che potresti disegnare avrebbe quattro angoli retti, ovvero questo spazio non ha quadrati o rettangoli. Un posto davvero strano!

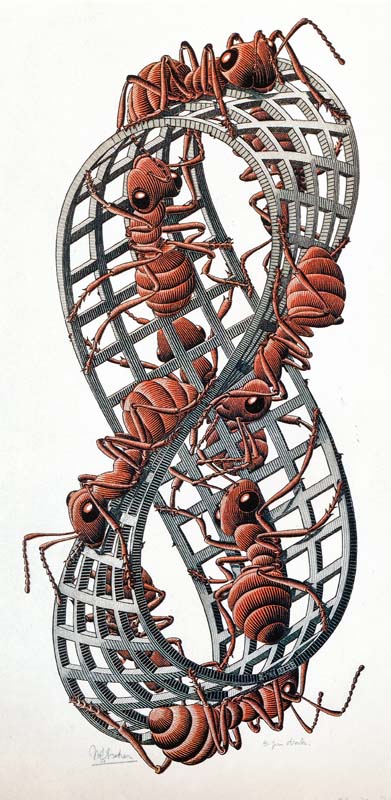
Oltre alle geometrie euclidee e non euclidee, Escher era molto interessato agli aspetti visivi della topologia, una branca della matematica che si occupa di quelle proprietà di uno spazio che non cambiano nonostante le distorsioni che possono allungarlo o piegarlo, ma che non lo strappano o lo perforano, e i topologi erano impegnati a mostrare al mondo strani oggetti curiosi. La striscia di Möbius è forse l’esempio principale, ed Escher ne ha fatto molte rappresentazioni. Essa ha la curiosa proprietà di avere solo un lato e un bordo. Quindi, se tracciate il percorso delle formiche nella striscia di Möbius II (figura sotto), scoprirete che non camminano affatto su lati opposti della striscia, ma camminano tutte sullo stesso lato. È facile realizzare una striscia di Möbius; basta tagliare una striscia di carta con le forbici, darle una mezza torsione e quindi incollare o scollare le estremità. Cosa prevedete che accadrà se provate a tagliare una striscia del genere in due, nel senso della lunghezza? SOLUZIONE A FONDO

La logica dello spazio

Con la “logica” dello spazio intendiamo quelle relazioni spaziali tra oggetti fisici che sono necessarie e che, quando violate, danno origine a paradossi visivi, a volte chiamati illusioni ottiche. Tutti gli artisti sono interessati alla logica dello spazio e molti ne hanno esplorato le regole in modo del tutto deliberato, come Picasso, per esempio. Un tipo di “disegno impossibile” si basa sull’insistenza del cervello nell’utilizzare indizi visivi per costruire un oggetto tridimensionale a partire da una rappresentazione bidimensionale. Escher ha creato molte opere che affrontano questo tipo di anomalia. Una delle più intriganti si basa su un’idea del matematico Roger Penrose: il triangolo impossibile (figura sotto). Appare come un solido costituito da tre prismi a base quadrata uniti tra loro con tre angoli retti a formare un triangolo. Ricordiamo che in geometria euclidea la somma degli angoli interni di un triangolo corrisponde a 180°, pertanto non può esserci più di un angolo retto.

Autoriferimento

L’ultimo dei concetti centrali (qui considerati) catturati da Escher è quello dell’autoriferimento, che molti ritengono sia il nocciolo dell’enigma della coscienza e della capacità del cervello di elaborare le informazioni in un modo che nessun computer è ancora riuscito a imitare con successo.

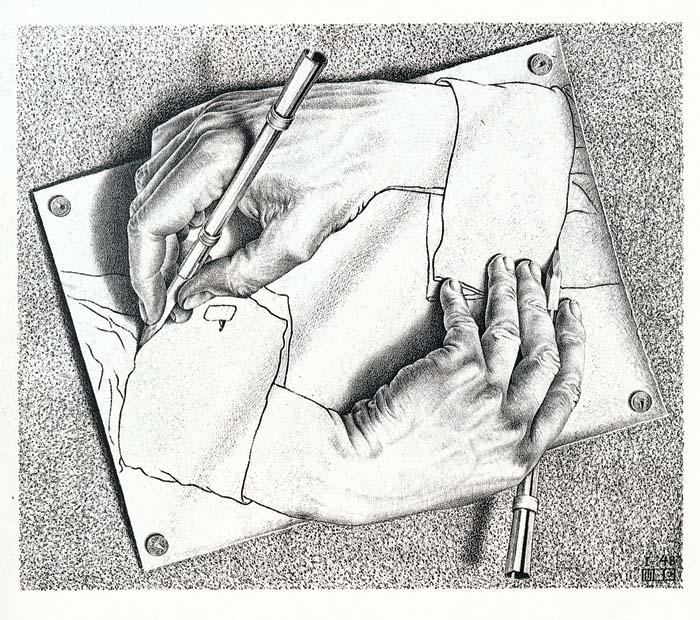
La litografia Drawing Hands (figura sotto) cattura questa idea.L ‘autoreferenzialità è diretta e concettuale; le mani si disegnano in modo molto simile a come la coscienza considera e costruisce se stessa, misteriosamente, con sé e autoreferenzialità inseparabili e co-uguali.

CONCLUSIONE

Molto di più potrebbe essere detto, ed è stato detto, sulla profondità, il significato e l’importanza dell’opera di Escher. A mio avviso egli non è un genio della matematica, ma un artista con una grandissima immaginazione e una capacità di visualizzazione geometrica fuori dal comune. Il connubio tra realismo, scienza e fantasia lo ha reso uno degli artisti più sorprendenti del Novecento e tutt’oggi crea stupore e curiosità negli occhi degli spettatori di ogni età.

SOLUZIONE: Invece di ottenere due strisce separate, otterrai una singola striscia lunga, che ha due torsioni e forma un anello più grande. Questo anello non è una nuova striscia di Möbius, ma piuttosto una striscia a due lati e due bordi intrecciati.

Bibliografia:

https://platonicrealms.com/minitexts/Mathematical-Art-Of-M-C-Escher

https://mcescher.com

All images may only be used unaltered, unchanged, and not manipulated in any way.