Dall’avvento delle teorie di Newton si pensava che il mondo funzionasse come un perfetto orologio svizzero, che scandiva le vite umane con estrema precisione e con un elevato grado di determinismo. Il meccanicismo si era radicato nella mente degli scienziati e nell’immaginario comune e garantiva un alto livello di sicurezza, in quanto era supportato da strumenti di Calcolo differenziale e integrale ( inventati proprio da Leibniz e Newton in quel periodo) e dalle leggi di Newton che governavano i fenomeni di meccanica celeste. Dal punto di vista filosofico la diretta conseguenza del determinismo causale è che,conoscendo le cause che hanno scatenato un evento, allora è possibile conoscere gli eventi successivi a partire dalla conoscenza delle configurazioni iniziali.
Questa teoria iniziò a vacillare grazie alle scoperte di Darwin sull’evoluzione della specie e della selezione naturale e sull’introduzione del concetto di entropia in termodinamica e sull’irreversibilità di molti fenomeni. Il meccanicismo non riusciva a spiegare la complessità di questi fenomeni. Per quanto riguarda il modello gravitazionale Newtoniano, fino agli anni ’60 del ‘900 rimaneva una buona approssimazione dei fenomeni osservabili, nonostante l’introduzione della Relatività Generale e della Meccanica Quantistica l’avessero privata del suo status di centralità.
La svolta avviene proprio nei primi anni 60′ del 900′ in un centro di ricerca americano per le osservazioni
meteorologiche grazie ad un evento casuale e, da quel momento, il termine ‘caos’ entrò a far parte del linguaggio scientifico. Il termine caos era usato nell’antica Grecia in opposizione al cosmos, ovvero l’ordine, ma come vedremo il suo utilizzo contemporaneo si basa sulla sua identificazione con fenomeni fisici, sociali o economici non spiegabili in maniera analitica. Ritornando agli anni 60′, Edward H. Lorenz, come molti altri meteorologi prima di lui, stava cercando di costruire dei modelli efficaci per prevedere il tempo. Basandosi su un set complesso di equazioni differenziali (di cui sotto inserisco una immagine senza commentare i vari termini, per mantenere l’articolo di carattere divulgativo) costruì un modello matematico e lo implementò sul computer attraverso metodi iterativi per approssimare le parti non lineari delle equazioni, ottenendo una particolare simulazione.
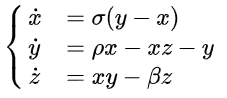
Successivamente ripetè la stessa simulazione approssimando non a 6 cifre decimali, ma solamente a 3 alcune variabili e la cosa sorprendente è che ottenne una previsione completamente diversa. Sconvolgente! Infatti in Fisica è ben noto che, se un evento avviene ad una determinata scala (spaziale o temporale), i fenomeni su scala inferiore sono quasi sempre trascurati. Ad esempio il moto di rotazione della Terra su se stessa non influisce sul moto di rivoluzione intorno al Sole, se non in maniera trascurabile. In questo caso, invece, una piccola variazione dei dati iniziali ha provocato una grande variazione del risultato… l’errore si è propagato in maniera esplosiva e dunque non è possibile prevedere alcunchè. L’errore osservato da Lorentz non è sperimentale, ma è definito come “effetto farfalla” e la potenza del suo concetto è racchiusa in una immagine metaforica, ormai divenuta ‘pop’: “Il battito d’ali di una farfalla in Brasile può causare un tornado in Texas”.
Le conseguenze dell’effetto farfalla minano il meccanicismo fino alle sue fondamenta. La logica Newtoniana imponeva che a piccole variazioni dei dati iniziali corrispondevano variazioni di errore controllate. Questo in realtà non accade sempre. Le leggi che regolano i fenomeni continuano ad essere deterministiche e valide, ma si può dire che non prevedano più nulla e che quindi non siano più operative.
Con Lorentz nasce la Teoria del Caos, che descrive dal punto di vista matematico le dinamiche caotiche dei cosiddetti sistemi complessi, le quali hanno alcune caratteristiche in comune, prima su tutte è l’estrema sensibilità ai dati iniziali, come si è potuto riscontrare nell’esperimento di Lorentz. Questa caratteristica rende imprevedibile e caotico il sistema, in quanto anche piccole imperfezioni nella conoscenza dei dati iniziali provoca la mancata predizione del fenomeno futuro, ed è anche per questo che i dati metereologici sono inutilizzabili dopo un certo tempo.
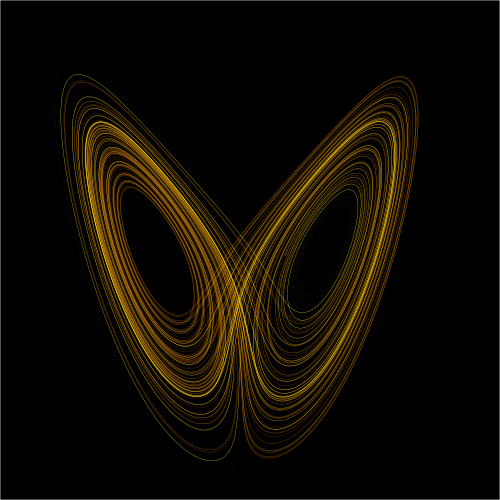
Un’altra caratteristica dei sistemi dinamici caotici è la presenza di attrattori strani.
Evitando di dare la definizione (che tra l’altro non è univoca) di sistema dinamico, affermo solamente che un sistema dinamico è rappresentato da una serie di grandezze che variano nel tempo e può essere figurato in uno spazio astratto, detto spazio delle fasi, dove sono presenti regioni nelle quali il moto del sistema è “catturato”, ovvero non può uscirne. Per maggiore chiarezza consideriamo il caso bidimensionale del pendolo reale: se fatto oscillare da una qualsiasi posizione iniziale, a causa dell’attrito, dopo un tempo più o meno lungo si posizionerà nel suo punto più basso e lì si stabilizzerà. Quel punto è un attrattore ( perchè,detto in maniera ingenua, “attrae” il pendolo (nel nostro caso) a raggiungere quella posizione e a rimanerci) e nella letteratura scientifica è definito come punto fisso. Altri attrattori sono i cicli limite, rappresentati da curve chiuse nel piano che il sistema percorrerà all’infinito con un determinato periodo senza poterne uscire, ma la grande scoperta di Lorentz fu di aggiungere a queste due tipologie di attrattori un terzo tipo: gli attrattori strani.
Quando un punto raggiunge una regione dove è presente un attrattore strano, rimane intrappolato in essa, descrivendo una curva particolare che si avvolge su se stessa senza mai intersecarsi in alcun punto. Man mano che scorre il tempo queste curve diventano più complesse, si stratificano e producono forme particolari, quelli che osservò Lorentz hanno un corpo centrale e due ali, simili ad una farfalla (forse anche da cui deriva il nome effetto farfalla?). Vedere immagine in copertina.
Ed è da questa immagine suggestiva che nasce il fortissimo interesse per la Teoria del Caos non solo nel mondo matematico/fisico, ma anche nel panorama culturale in generale, diventando quasi una tematica pop. Siccome il mio obiettivo ( non troppo velato oramai) è mostrare come si possa creare una cultura scientifica e renderla interdisciplinare, citerò un paio di film che trattano e sviluppano questo tema:
Mr. Nobody (2009): film fantascientifico diretto da Jaco Van Darmael, segue la storia di Nemo Nobody, uomo di 118 anni, ultimo essere umano mortale dopo che la specie umana ha raggiunto l’immortalità. Nemo, con ricordi sbiaditi, racconta delle sue principali storie d’amore, del divorzio dei suoi genitori e delle successive difficoltà incontrate in tre momenti della sua vita: all’età di nove, quindici e trentaquattro anni. L’aspetto confusionario della storia è dato dalla presenza di più linee narrative, ognuna delle quali racconta un percorso di vita alternativo. Il film utilizza una narrativa non lineare e l’interpretazione a molti mondi (di cui ho parlato nello scorso articolo) per raccontare la storia della vita di Nemo. L’effetto farfalla è presente in questo film nella struttura stessa della trama e nelle sue diramazioni. Non dirò oltre per non spoilerare troppo, lascio qui sotto un brevissimo estratto del film che potrà mostrarvi quanto forte sia la presenza di questo concetto nel film.
Sliding Doors: film del 1998 che ha come protagonista Helen, una giovane donna che, arrivata tardi in ufficio, scopre di essere stata licenziata e infuriata corre verso la stazione del treno. Da questo momento la sua vita si svilupperà su due piani paralleli, determinati da un gesto insignificante: aprire la porta del treno. Nel primo scenario Helen prende la metro e torna a casa in tempo per scoprire il tradimento del fidanzato, ma da questo evento riuscirà a riprendersi e a vivere una nuova storia d’amore felice, mentre nel secondo scenario non la prende e, tornando a casa tardi, non scopre il tradimento in quel momento, ma la sua vita avrà dei risvolti negativi e le provocherà infelicità.

In matematica quando il comportamento di un sistema dinamico cambia
radicalmente per alcuni valori dei parametri di controllo, si dice che per quel valore è occorsa una
biforcazione.
Quello che ci insegna dunque l’effetto farfalla e la teoria del caos in generale è che non possiamo sapere come le nostre azioni possano influenzare la nostra vita o la storia dell’umanità, ma è bene essere consapevoli e responsabili del fatto che sicuramente una nostra azione ne influenzerà una più grande. Questo monito dovrebbe essere presente in ognuno di noi… sicuramente maggiore è il potere a disposizione maggiore è l’attenzione che si dovrebbe porre (“Da grandi poteri derivano grandi responsabilità”) e rileggendo questa frase alla luce degli eventi geopolitici e sociali che ci circondano di questi tempi, diventa profondamente attuale. Ma per parlare di ciò ci sarà spazio in un prossimo articolo probabilmente 🙂