Intorno al VI secolo d. C si sviluppò in India un gioco strategico chiamato chaturanga, il precursore diretto del gioco degli scacchi moderni, le cui regole furono standardizzate solo alla fine del XIX secolo. Riconosciuto come sport dal Comitato Olimpico Internazionale, richiede grande concentrazione, abilità logiche, capacità di calcolo e gestione delle emozioni per poter essere praticato ad un buon livello. Per i neofiti diamo una breve descrizione di questo gioco:
- Si gioca in due, bianco e nero e il bianco ha la prima mossa
- Il tabellone di gioco è composto da 64 caselle (8×8)
- I pezzi iniziali per giocare sono: 8 pedoni, 2 torri, 2 alfieri, 2 cavalli, 1 regina e 1 re
- Lo scopo del gioco è dare scacco matto al re dell’avversario, ovvero ad intrappolarlo in modo che non possa eseguire più mosse legali per evitare la cattura
Quello che rende un gioco di strategia come gli scacchi popolare, sorprendente e mai banale o noioso è la matematica che fa da sostrato. Si può intuire immediatamente che in un quadrato 8×8 e con 16 pezzi che possono fare vari tipi di movimenti il numero di diverse combinazioni di mosse può essere elevato, ma scommetto che nessuno, senza aver fatto un calcolo precedentemente, possa davvero immaginare di quale ordine di grandezza si sta parlando. Lo vedremo a breve. Ogni combinazione di mosse influenza il processo decisionale dei giocatori, in base a strategie, compromessi e valore di ogni pezzo. Alcuni matematici famosi, come Eulero e Gauss, e scacchisti professionisti hanno scritto pagine e pagine sulle strategie ottimali, dando forma a quella che viene denominata come “teoria degli scacchi”. Essa si divide in 3 fasi: l’apertura, il mediogioco e il finale.
Sono state elencate e classificate 1327 varianti e sottovarianti di apertura differenti, che si possono ricollegare, a volte, l’una con l’altra in base a trasposizione di mosse. Ogni apertura è una serie di mezze mosse eseguite da ciascun giocatore, che si traducono in configurazioni diverse della scacchiera. La mossa completa è eseguita quando entrambi i giocatori hanno fatto una mezza mossa, ovvero hanno mosso un pezzo. La tabella seguente mostra l’incredibile varietà di partite possibili in base al numero di mezze mosse e dunque la complessità di questo gioco:
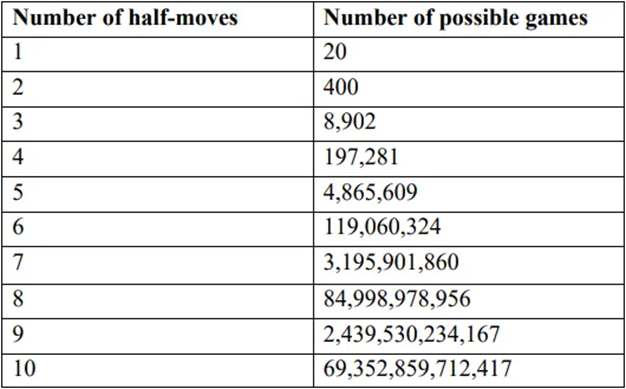
Come si può vedere, all’inizio il bianco ha 20 opzioni diverse per iniziare la partita ( 16 opzioni per gli 8 pedoni+ 4 opzioni per i cavalli), poi il nero può rispondere con altrettante 20 opzioni. Dopo una mossa completa siamo dunque già a 400 varianti. In sole 10 mezze mosse (quindi 5 mosse complete), si possono giocare
69 352 859 712 417 partite diverse… questa esplosione di numeri ha una forma esponenziale e rappresenta la caoticità di questo sistema di gioco, che per la mente umana si rivela di impossibile memorizzazione. Mediamente un giocatore esperto può memorizzare 15/20 mosse di ogni apertura, il che ne fa di per sé già un incredibile calcolatore umano!
In un articolo “Programming a Computer for Playing Chess” del 1950, il matematico americano Claude Shannon stimò l’esistenza di 10^(120) diverse varianti di gioco. Questo numero è stato calcolato su una durata media a partita di 40 mosse e considerando il fatto che ogni giocatore può effettuare mediamente 30 mosse legali per turno, 30×30=900 (circa 1000= 10^3) possibili varianti in una mossa, allora in 40 mosse avremo 10^120 partite differenti.
Secondo gli scienziati il numero di atomi nell’universo è circa 10^(80), dunque il numero di partite possibili in 40 mosse è circa 40 volte più grande… direi sorprendente e affascinante!
Ovviamente questo numero di Shannon tiene conto di tutte le possibili mosse, anche quelle assurde o controproducenti che fanno perdere la partita; una stima più sensata e concreta è data dal fatto che un giocatore abbia in media circa tre mosse ragionevoli nel suo turno, quindi ogni mossa completa avrà 3×3=9 varianti e il numero di partire sensate sarà 10^(40)..un numero in ogni caso immenso.
Se tutti noi nel mondo ci mettessimo in coppia e giocassimo un partita diversa ogni giorno, impiegheremmo trilioni di anni per giocare tutte le partite sensate possibili.
A questo punto entra di prepotenza l’elefante nella stanza rappresentato dall’ IA. I supercomputer sono stati creati per elaborare enormi quantità di dati in poco tempo ed eseguire calcoli complessi, dunque perfetti per imparare il gioco degli scacchi. La prima volta che il computer superò (definitivamente) l’essere umano, fu nel 1997 quando Deep Blue sconfisse Garry Kasparov, fortissimo scacchista russo e campione del mondo di quell’anno. Quella fu nella storia degli scacchi l’inizio di una nuova era, improntata sull’utilizzo di strumenti di calcolo virtuali per l’apprendimento del gioco degli scacchi. Ad oggi tutti gli scacchisti si servono dell’IA per analizzare le loro partite, imparare nuove aperture e strategie per migliorare. Nessun essere umano potrà raggiungere il livello di gioco di questi programmi, quali Stockfish o Leela.
Mi avvicino alla conclusione di questo articolo parlando brevemente di quali siano le tecniche di apprendimento di Deep Blue, che ha segnato, come detto in precedenza, l’alba dell’era dei computer negli scacchi:
- Decision tree: il computer cerca in ogni configurazione della scacchiera le mosse legali
- Evaluation function: una funzione matematica che prende in input un certo stato e restituisce un punteggio (il valore assegnato ai pezzi) come output. Per il giocatore in questione, considera tutti i pezzi di entrambi i giocatori, verifica il punteggio assegnato a ciascun pezzo di ogni giocatore e restituisce un punteggio complessivo che rappresenta la sua probabilità di vittoria.
- Minimax algorithm: algoritmo che ha lo scopo di minimizzare la massima “perdita” dovuta ad una mossa, data la disposizione della scacchiera. Questo algoritmo prevederà, in base alla potenza di calcolo del computer, quali mosse consentono al giocatore di aumentare le sue possibilità di vittoria e le presenterà come mosse migliori.
- Optimization: tecnica essenziale per eliminare i calcoli ripetitivi in un decision tree e di risparmiare dunque potenza di calcolo e tempi di elaborazione di risposta.
In questo articolo sono state presentate dunque a grandi linee le tecniche matematiche di machine learning utilizzate dall’IA per apprendere in maniera profonda il gioco degli scacchi, si è visto in maniera chiara il caos dovuto ad un numero enorme di possibilità diverse in cui il gioco può svilupparsi e la sua complessità intrinseca.
Vorrei concludere l’articolo con un invito a provare ad imparare a giocare a scacchi, perché a mio avviso può portare grandi benefici in termini di concentrazione, gestione dell’ansia e per implementare le proprie capacità logiche e di memorizzazione, basandosi il gioco su intuizione e calcolo. Ovviamente può essere estremamente stressante e a volte frustrante, banalmente basta un singolo errore per perdere una partita, ma giocare a livelli amatoriali non può farvi sicuramente male! Alla prossima 😊
Riferimenti:
https://jng15.medium.com/chess-math-to-check-mate-the-mathematics-of-chess-2b1ee5eacb18





